In this semester-long course, students will explore, discover, and prove fundamental properties of the lattice plane. We will formulate and prove a necessary and sufficient condition for constructing a regular lattice polygon with n sides and, along the way, will discover a range of unexpected and interesting properties of lattice point geometry. These include results on the algebraic structure of the lattice plane, Pick’s Theorem, Blichfeldt’s Theorem, Minkowski’s Theorem, and a variety of others. This course provides a rich opportunity for students to discover the many, and often surprising, interrelations between seemingly disparate areas of mathematics. We will engage rigorously with deep mathematical concepts, including a number of topics not typically studied at the secondary or undergraduate levels. This culminating course will involve work in a range of mathematical fields, including number theory, linear algebra, graph theory, and abstract algebra. Students will participate actively in the mathematical development process, beginning with questions that are easy to state and investigate empirically, and ultimately reaching open areas of research in mathematics.
Course Number
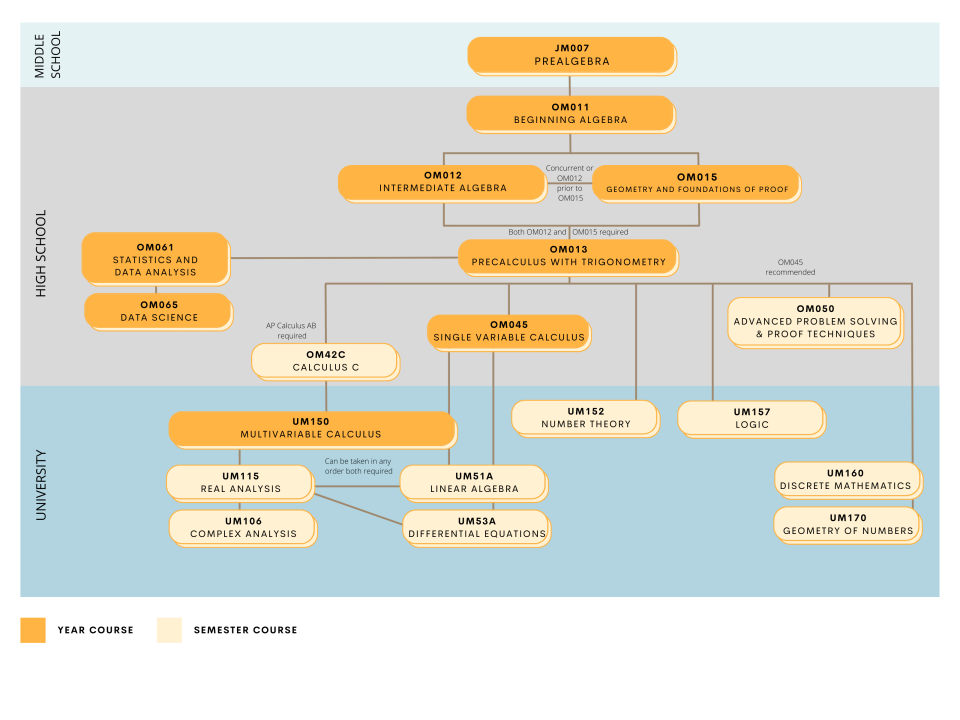
UM170
Level
University
Semester
Spring
Credit Hours
5.00
Subject
Prerequisites
Discrete Mathematics (UM160), or consent of the instructor. Familiarity with reading and writing mathematical proofs is expected.